The Rambling Programmer

Binary Search Trees

Data Structures & Algorithms

You down with BST? Yeah, you know me. Your not down with BST’s you say? Well get ready, your about to be. Last week we talked about Trees in general. This week we are going to narrow our focus and look at Binary Search Trees. So if you need to brush up on Trees in general you can do that here.

A Binary Search Tree, BST from here on out, is simply a tree with the additional property that it’s keys are in sorted order. That is, any Nodes or sub-trees on the left branch of a Node are less than the Node and any Nodes or sub-trees on the right branch of a Node are greater than the Node. See the picture below for clarification.

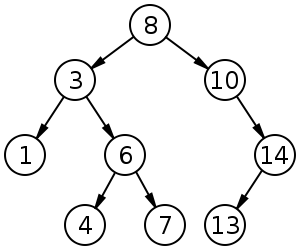
Notice how all the values to the left of the Root Node, 8, are less than 8 and all the values in the right sub-tree are greater than 8. This property holds for all sub-trees of the Tree as well. This single property, allows for speedy search, insert and delete methods, all three of which have average runtimes of O(log n).

Let’s get started writing some code. First off we need to implement a Node class. It should have a value and pointers to left and right nodes:

class Node
  attr_accessor :key, :left, :right

  def initialize(key)
    @key = key
    @left = nil
    @right = nil
  end
end

Pretty straightforward, our class initializer simply sets the value of the Node and the left and right pointers are set to nil.

Next, we should implement the BST class. This will also be fairly simple, as far as initialization goes. We are simply going to create a root that is set to nil. Now that’s great and all, but we can’t really do anything with it, so we will also implement an insert method at the same time which will allow us to insert Nodes into our new BST class.

class BST
  attr_accessor :root

  def initialize
    @root = nil
  end

  def insert(key)
    insert_node(@root, key)
  end

private

  def insert_node(current_node, key)
    if current_node.nil?
      current_node = Node.new(key)
    elsif key < current_node.key
      insert_node(current_node.left, key)
    elsif key > current_node.key
      insert_node(current_node.right, key)
    end
  end
end

A few things to note here. The insert method delegates to a private method, insert_node. The real work is done in the insert_node method, which compares the value that needs to be inserted to the current_node, if it is less than, we recursively call insert_node on the left child and vice-versa if it is greater, until we find an empty Node, at which point we insert a new Node.

Great, so we can build out a BST by simply creating a new BST with BST.new. The we insert nodes one by one with the insert method, passing it a key value. The next step is to implement a search method that will allow us to traverse the BST and determine if a Node with a certain key value exists.

class BST
  attr_accessor :root

  def initialize
    @root = nil
  end

  def insert(key)
    insert_node(@root, key)
  end

  def search(key)
    find_node(@root, key)
  end

private

  def insert_node(current_node, key)
    if current_node.nil?
      current_node = Node.new(key)
    elsif key < current_node.key
      insert_node(current_node.left, key)
    elsif key > current_node.key
      insert_node(current_node.right, key)
    end
  end

  def find_node(current_node, key)
    if current_node.nil?
      return nil
    end

    if current_node.key == key
      return current_node
    elsif key < current_node.key
      find_node(current_node.left, key)
    elsif key > current_node.key
      find_node(current_node.right, key)
    end
  end
end

Much like we did with the insert method, we delegate to a private method called find_node. This method starts out checking for two potential base cases, either the current_node is nil, in which case we return nil, or the current_node.key is equal to the key we are searching for, in that case we found what we are looking for and return it. Otherwise we recursively traverse the tree based on whether the key we are looking for is less than or greater than the current_node.key , just like we did in the insert method. This is a pattern you are going to see over and over in Trees. Since Trees are a recursive structure, we typically traverse them recursively.

Finally, we will implement a delete method. This is slightly more challenging than the insert and search methods. Once we find the Node we are looking for there are basically three cases to consider.

• The node has no children
• The node has either a left child or a right child
• The node has both right and left children

The first two are fairly straightforward. If the Node has no children we simply remove it. If the Node has only one child we remove the Node and replace it with its child. If the Node has two children we find it’s next successor in the Tree. This Node can be found by taking the right sub-tree and finding the minimum value in it. See the image below again.

In the instance we want to remove the Node whose value is 3, we would find its successor. To do this we would find the smallest value in its right sub-tree. In other words we go to the right child, the Node whose value is 6 and then traverse the Tree to the left until we find a leaf node, which is the Node whose value is 4. We then replace the 3 with 4 and remove the leaf Node. Let’s see the code.

class BST
  attr_accessor :root

  def initialize
    @root = nil
  end

  def insert(key)
    insert_node(@root, key)
  end

  def search(key)
    find_node(@root, key)
  end

  def delete(key)
    delete_node(@root, key)
  end

private

  def insert_node(current_node, key)
    if current_node.nil?
      current_node = Node.new(key)
    elsif key < current_node.key
      insert_node(current_node.left, key)
    elsif key > current_node.key
      insert_node(current_node.right, key)
    end
  end

  def find_node(current_node, key)
    if current_node.nil?
      return nil
    end

    if current_node.key == key
      return current_node
    elsif key < current_node.key
      find_node(current_node.left, key)
    elsif key > current_node.key
      find_node(current_node.right, key)
    end
  end

  def delete_node(current_node, key)
    if current_node.key == key
      remove_node(current_node)
    elsif current_node.key < key
      delete_node(current_node.left, key)
    elsif current_node.key > key
      delete_node(current_node.right, key)
    end
  end

  def remove_node(node)
    # Case 1: No children
    if node.left.nil? && node.right.nil?
      node = nil
    # Case 2: One child
    elsif node.right.nil? && !node.left.nil?
      node = node.left
    elsif node.left.nil? && !node.right.nil?
      node = node.right
    else
      node = replace(node)
    end
  end

  def replace(node)
    node.value = successor(node.right)
    node.right = update(node.right)
  end

  def successor(node)
    if !node.left.nil?
      successor(node.left)
    end

    return node.key
  end

  def update(node)
    if !node.left.nil?
      node.left = update(node)
    end

    return node.right
  end
end

So there is a lot of new code here, let’s go through it. Like before the delete method is simply an interface method, that delegates to delete_node. delete_node should look familiar it simply traverses the tree searching for the node to be deleted, much like we did with the insert and search methods. Once we find it we call the remove_node method which evaluates the three methods we discussed above.

If the Node has no children it simply sets it to nil. If it has only one child it sets it to that child. Finally, if it has two children we call the replace method using the Node’s right child. The replace method takes advantage of the successor and update methods to find the next successor, and update the Nodes appropriately.

This is really only the most basic implementation of a BST. I encourage you to look into traversals: in-order, pre-order, and post-order. Perhaps extend the code above to print out the tree using these traversal methods. You can also consider implementing a method that returns the height of your tree, whether or not the tree is balanced, or the number of Nodes in the tree. The possibilities are endless. Thanks for reading, below are some further study resources. Until next time.

Binary search tree - Wikipedia
Binary Search Tree | Set 1 (Search and Insertion) - GeeksforGeeks