Graphs
Data Structures & Algorithms
Our journey has taken us far. We started off with basic search algorithms and recursion. Soon we moved on to some basic data structures like Linked Lists, Stacks and Queues. Lately our focus has been on Trees, including Binary Search Trees and methods to traverse them. We haven’t exhausted Trees by a long shot, perhaps we will circle back around and take a deeper dive but for now it’s time to move on.
What’s next you might be asking, actually, you probably aren’t asking that at all since you read the title of this post. Graphs are the next logical step in our journey, since a Tree is a very specific type of Graph. In fact, a Tree is an Undirected Graph that has no cycles. This may not make sense right now but we will discuss these terms shortly.
A Graph is an abstract data type in computer science that has an entire field of study associated with it, called graph theory. As such, we won’t be able to cover every detail regarding Graphs.
Graphs have the same basic components as Trees, Nodes and Edges or Directed Edges. This makes sense, since a Tree is just a very specific type of Graph.
There are two broad types of Graphs:
- Directed Graph — A Directed Graph is one whose Edges have direction. These directions can be one or two ways and are often called Directed Edges. See the example below.
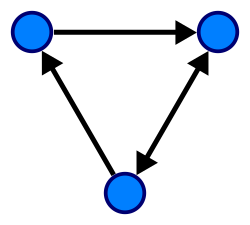
- Undirected Graph — As it’s name implies, an Undirected Graph is one in which the edges have no direction.
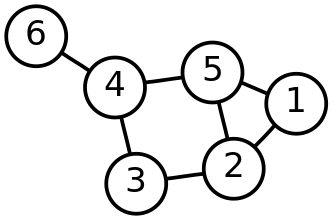
Graphs may also contain cycles, or not. For example the sequence of Nodes from the Example 2 above, 4–5–2–3–4, is a cycle because the first Node is reachable from itself. There are several other cycles in this Graph as well, 5–1–2–5, is another example. Also 3–4–5–1–2–3.
A cycle graph is a Graph that is a cycle in it’s entirety. The below image is an example of the most basic Cycle Graph. Notice how each Node has degree 2, that is it each Node has two Edges emanating from it. This is true of all Cycle Graphs.

A Graph my also be a Complete Graph. A Complete Graph is one in which each Node is connected to all other Nodes. In the image below notice how there are 5 Nodes and each Node has degree of 4. All Nodes in a Complete Graph will have degree of, # Nodes - 1.

One last category of Graph worth mentioning is a Weighted Graph. A Weighted Graph is one in which a value is assigned to each Edge. These graphs are common in many types of CS problems, including shortest path problem which you are probably familiar with thanks to Google Maps or Waze.
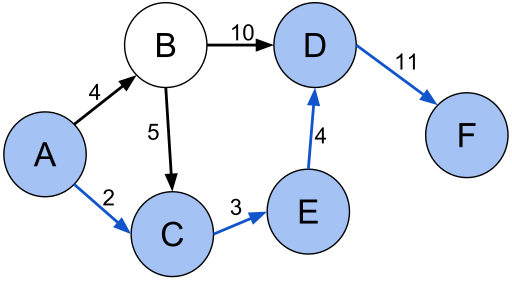
That’s a pretty quick and dirty overview of Graphs. Next time we will start to implement a graph data structure and some of the algorithms associated with it. Some of those algorithms worth considering are adding and removing Nodes, adding and removing Edges, and testing whether two Nodes are neighbors, just to name a few.
Below is some further reading material covering some of the topics we talked about in this post as well as some more advanced topics we didn’t cover. Until next time and thanks for reading along.
Graph (abstract data type) - Wikipedia
Graph (discrete mathematics) - Wikipedia
Travelling Salesman Problem - Wikipedia