Trees
Data Structures & Algorithms
Of course we all know the old saying, “Trees, trees, the musical fruit…”. That doesn’t look quite right, oh well. We have made some serious progress in our quest to better understand CS basics from a web developers perspective. We’ve implemented Merge and Insertion Sorts. We’ve delved into data structures like Linked Lists, Stacks, and Queues. Now it’s time to climb out way up into Trees. There won’t be any coding in this post, there is simply too much information to cover and understand before we actually implement any kind of tree, whether it be a Binary Tree, Binary Search Tree, Red-Black Tree, N-ary Tree or any other type. Don’t worry if those names don’t make sense to you now, they will, after we cover the basics.
So what is a Tree in computer science? Very simply, a Tree is a data structure made up of Nodes and Edges that does not have a cycle. Ok, so what does that mean? Let’s break it down. We are familiar with Nodes thanks to linked lists, nothing has changed. A node simply contains a value or data and a link or links to other Nodes. An Edge is the link between two nodes. Makes sense, what does it mean to not have a cycle though? Well a Cycle is a path of Edges and Nodes in which a Node is reachable from itself. Take a look at the image below.

The collection of nodes (A, B, C, …) is cyclic, that is, it contains a loop. Notice how node B can be reached by following the path created by B -> C -> E -> D -> B. This collection is therefore NOT a Tree. Keeping that in mind let’s look at another image.
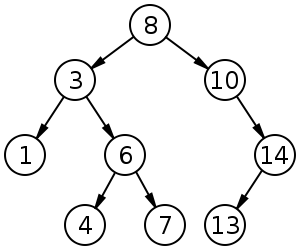
This is a Tree. Specifically, this is a Binary Tree. A Binary Tree is simply a Tree whose Nodes contain at most 2 children. Wait a minute, what are children? That’s a good question, let’s define some of the terminology used when talking about Trees. Keep the above image in mind while we do this.
- Root — The topmost Node in a Tree. In the example above the Node whose value is 8 .
- Edge — A connection between one node and another. The arrows in the image above.
- Child — A Node which is directly connected to another Node when moving away from the Root. Nodes 3 and 10 are Children of Node 8 above. Node 13 is a Child of Node 14 as well.
- Parent — A Parent is the opposite of a Child. The Parent of Node 1 is Node 3. Any Node in the Tree will have only one Parent.
- Sibling — A group of Nodes that have the same Parent. Nodes 1 and 6 are siblings, they have a common parent Node 3.
- Leaf — A node with no Children. Nodes 1, 4, 7, and 13 are Leaf Nodes.
Let’s take some of this terminology and talk about the characteristics of Binary Trees. A Binary Tree, as mentioned above is a Tree whose Nodes have at most 2 Children. The example image above is an example of a Binary Tree. Binary Trees have the interesting property that they have one less Edge than they have Nodes. The image above has 9 Nodes and 8 Edges. This is true of all well formed Binary Trees. Cool!
Binary Trees are also recursive in nature. The subtrees are similar to the Tree in the sense that they have a Root and potentially, that Root has at most two Children, who can themselves be the Root of a subtree. In the coming weeks as we start to implement these data structures and the algorithms to manipulate them you will see that recursion is everywhere. So if you are a little rusty on recursion go back and freshen up here.
We can also classify Binary Trees based on some of their characteristics.
- Full Binary Tree — A Tree where every node has either 0 or 2 children.
- Complete Binary Tree — A Tree where every level is completely filled, except for the last. In the last level all Nodes are as far left as possible. (Note: The Full Tree below is also a Complete Tree, it simply doesn’t need to have a last level that isn’t completely filled due to the number of nodes.)
- Binary Search Tree — A Binary Search Tree is a Binary Tree that its order in such a way that every Left Child’s value is less than it’s Parent’s Value, and every Right Child’s value is greater than it’s Parent’s Value. (Neither of the two examples below are BSTs, notice the Left Child of the Root Node is greater than the Root, that is 2 > 1. The example above that we used for defining a Tree and it’s terminology is a BST.)

That’s a lot to wrap your head around if you have never seen Trees before. Make sure you have a good understanding of this to ensure a good foundation moving forward into implementation. Below are some additional links to further your knowledge.
Tree (data structure) - Wikipedia
Binary tree - Wikipedia
Binary search tree - Wikipedia